For those of you who have been reading posts and checking out my artwork for a while, I have a small present. I have posted the full-sized versions of much of my special artwork from this blog on Pinterest.
You can get to it here.
Finally, if you click on into them, you can see the details and get an idea of how many hours I spent on these pieces. Sometimes a bit of work was so complicated it took several days to complete. Which totally explains why my posts take so long!
Enjoy!
I have other boards on Pinterest, some with cool patterns, clouds, and collections of things. Just a hobby, and I thought I'd share a bit.
Mark Zimmer: Creativity + Technology = Future
Please enter your email address and click submit to follow this blog
Showing posts with label artwork. Show all posts
Showing posts with label artwork. Show all posts
Thursday, June 6, 2013
Sunday, June 2, 2013
Mastering Nature's Patterns: Basalt Formations
I love patterns. This all originally stems from my observations of nature's patterns. A lot of the objects I draw (and develop in code mathematically) come directly from nature.
Strikingly, nature will often conspire to produce objects of great beauty, ones which we cannot match without tremendous effort. An example of this are the basalt formations. Created by volcanic upwelling, great pressure leading to crystallization, and fracturing during cooling, they are nature's brilliant tessellations, awe-inspiring extrusions, and mad ravings simultaneously.
They resemble three-dimensional bar graphs. Their fracture pattern, in two dimensions, is a natural Voronoi diagram. I first saw this pattern in nature while observing the way that soap bubbles join. Without fully understanding it, this observation introduced me to the mathematical laws of geometry when I was very young. Little did I know that I would never stop trying to duplicate it.
In this post, I show you how I duplicated this particular kind of nature. And I did it in my style, as you can see.
 To create a drawing of a basalt formation, I actually used a rendered Voronoi diagram, which you see here, transformed it into a subtle perspective, establishing two vanishing points. Then I made three copies arranged as layers in a way that approximated placing them on three-dimensional transparent layers at various depths. This was so I could see the levels, and so the third vanishing point could be right.
To create a drawing of a basalt formation, I actually used a rendered Voronoi diagram, which you see here, transformed it into a subtle perspective, establishing two vanishing points. Then I made three copies arranged as layers in a way that approximated placing them on three-dimensional transparent layers at various depths. This was so I could see the levels, and so the third vanishing point could be right.
Of course, I used Painter's Free Transform to do this!
I kept each layer a little bit transparent so I could get an intuitive feeling for which layer was on the top and which layer was on the bottom. This technique is called depth-cueing.
As you can see, it worked pretty well. I stopped at three layers because I didn't want the drawing project to get too complicated. But, of course, like all of my projects, it soon did!
 Next, on a new layer, I drew lines on top of the the lines that I wanted to represent the three-dimensional surface of the basalt formation. This meant choosing a three-dimensional height for each cell. The base layer that extended to the outside of the drawing was the lowest height, of course, and a second and third layer was built on top of it.
Next, on a new layer, I drew lines on top of the the lines that I wanted to represent the three-dimensional surface of the basalt formation. This meant choosing a three-dimensional height for each cell. The base layer that extended to the outside of the drawing was the lowest height, of course, and a second and third layer was built on top of it.
This causes cells to raise out of the base layer and appear to become extruded.
When I consulted some real images of basalt formations as a guide, I found that they were quite imperfect and usually were cracked, damaged, or eroded in some way.
I really wanted my drawing to represent a perfect un-eroded result.
 I used an extra transparent layer (behind the layer with the lines) and marked each cell with a three-dimensional height index so I could be sure which heights corresponded with each cells. This told me where to put the shading and also told me how to interpret the extrusion lines.
I used an extra transparent layer (behind the layer with the lines) and marked each cell with a three-dimensional height index so I could be sure which heights corresponded with each cells. This told me where to put the shading and also told me how to interpret the extrusion lines.
This layer was for informational purposes only. You see here the original small layer with crudely drawn lines. It's actually kind of hard to see the three-dimensional relative positions of the cells in some cases, which is another reason I labelled each cell with a height index.
Once I had designed it, I found that the drawing was way too small to shade the way I like to (using a woodcut technique) and so I resized the image and went over each of the lines by hand to make it crystal clear at the new resolution.
 That only took a few days.
That only took a few days.
Why? After resizing the image, I found that each line was unusually soft. This meant that I had to go over the lines with a small brush, darkening and resolving the line. Then I had to go around it with white to create a clean edge. This is what really took the time!
Naturally I do lots of other things than just draw all the time, and so I had to use extra minutes here and there. I kept the Painter file on my laptop and brought my Wacom tablet with me in my bag.
I spent probably ten or twenty hours drawing this image.
Once the lines were perfect, the next step was shading. But of course it had to be in my style, and this also took quite a bit of time.
 I used woodcut shading to create shadows and accessibility shading. This created a very nice look.
I used woodcut shading to create shadows and accessibility shading. This created a very nice look.
To do this, I drew parallel lines at a desired spacing, taking care to make them correspond in length and position to the shading and shadows that would result from a light coming from the left side.
I thickened the lines at their base, and made them a bit triangular. Then at the end, I used a small white brush to erode and sharpen the point and clean the sides of each shading line to get the right appearance.
 The final step was coloring the tops and the sides, using a gel layer.
The final step was coloring the tops and the sides, using a gel layer.
I colored each layer using a different shade of slightly bluish gray. The top layer got the lightest shade.
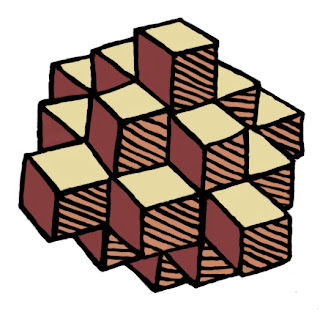
Here you can see a close-up of the final image, which was very high resolution indeed.
Even though I started out with a computer-generated fracturing pattern, I was able to retain a hand-wrought look to the final image. None of the lines are really computer-prefect
Yes, nature's patterns often take a bit of time to master!
Strikingly, nature will often conspire to produce objects of great beauty, ones which we cannot match without tremendous effort. An example of this are the basalt formations. Created by volcanic upwelling, great pressure leading to crystallization, and fracturing during cooling, they are nature's brilliant tessellations, awe-inspiring extrusions, and mad ravings simultaneously.
They resemble three-dimensional bar graphs. Their fracture pattern, in two dimensions, is a natural Voronoi diagram. I first saw this pattern in nature while observing the way that soap bubbles join. Without fully understanding it, this observation introduced me to the mathematical laws of geometry when I was very young. Little did I know that I would never stop trying to duplicate it.
In this post, I show you how I duplicated this particular kind of nature. And I did it in my style, as you can see.
 To create a drawing of a basalt formation, I actually used a rendered Voronoi diagram, which you see here, transformed it into a subtle perspective, establishing two vanishing points. Then I made three copies arranged as layers in a way that approximated placing them on three-dimensional transparent layers at various depths. This was so I could see the levels, and so the third vanishing point could be right.
To create a drawing of a basalt formation, I actually used a rendered Voronoi diagram, which you see here, transformed it into a subtle perspective, establishing two vanishing points. Then I made three copies arranged as layers in a way that approximated placing them on three-dimensional transparent layers at various depths. This was so I could see the levels, and so the third vanishing point could be right.Of course, I used Painter's Free Transform to do this!
I kept each layer a little bit transparent so I could get an intuitive feeling for which layer was on the top and which layer was on the bottom. This technique is called depth-cueing.
As you can see, it worked pretty well. I stopped at three layers because I didn't want the drawing project to get too complicated. But, of course, like all of my projects, it soon did!
 Next, on a new layer, I drew lines on top of the the lines that I wanted to represent the three-dimensional surface of the basalt formation. This meant choosing a three-dimensional height for each cell. The base layer that extended to the outside of the drawing was the lowest height, of course, and a second and third layer was built on top of it.
Next, on a new layer, I drew lines on top of the the lines that I wanted to represent the three-dimensional surface of the basalt formation. This meant choosing a three-dimensional height for each cell. The base layer that extended to the outside of the drawing was the lowest height, of course, and a second and third layer was built on top of it.This causes cells to raise out of the base layer and appear to become extruded.
When I consulted some real images of basalt formations as a guide, I found that they were quite imperfect and usually were cracked, damaged, or eroded in some way.
I really wanted my drawing to represent a perfect un-eroded result.
 I used an extra transparent layer (behind the layer with the lines) and marked each cell with a three-dimensional height index so I could be sure which heights corresponded with each cells. This told me where to put the shading and also told me how to interpret the extrusion lines.
I used an extra transparent layer (behind the layer with the lines) and marked each cell with a three-dimensional height index so I could be sure which heights corresponded with each cells. This told me where to put the shading and also told me how to interpret the extrusion lines.This layer was for informational purposes only. You see here the original small layer with crudely drawn lines. It's actually kind of hard to see the three-dimensional relative positions of the cells in some cases, which is another reason I labelled each cell with a height index.
Once I had designed it, I found that the drawing was way too small to shade the way I like to (using a woodcut technique) and so I resized the image and went over each of the lines by hand to make it crystal clear at the new resolution.
 That only took a few days.
That only took a few days.Why? After resizing the image, I found that each line was unusually soft. This meant that I had to go over the lines with a small brush, darkening and resolving the line. Then I had to go around it with white to create a clean edge. This is what really took the time!
Naturally I do lots of other things than just draw all the time, and so I had to use extra minutes here and there. I kept the Painter file on my laptop and brought my Wacom tablet with me in my bag.
I spent probably ten or twenty hours drawing this image.
Once the lines were perfect, the next step was shading. But of course it had to be in my style, and this also took quite a bit of time.
 I used woodcut shading to create shadows and accessibility shading. This created a very nice look.
I used woodcut shading to create shadows and accessibility shading. This created a very nice look.To do this, I drew parallel lines at a desired spacing, taking care to make them correspond in length and position to the shading and shadows that would result from a light coming from the left side.
I thickened the lines at their base, and made them a bit triangular. Then at the end, I used a small white brush to erode and sharpen the point and clean the sides of each shading line to get the right appearance.
 The final step was coloring the tops and the sides, using a gel layer.
The final step was coloring the tops and the sides, using a gel layer.I colored each layer using a different shade of slightly bluish gray. The top layer got the lightest shade.
Here you can see a close-up of the final image, which was very high resolution indeed.
Even though I started out with a computer-generated fracturing pattern, I was able to retain a hand-wrought look to the final image. None of the lines are really computer-prefect
Yes, nature's patterns often take a bit of time to master!
Saturday, March 16, 2013
Five-Fold Symmetry
 Nature is replete with five-fold symmetry, thanks to five-petaled flowers. While most of the works of humankind are designed around 4-fold symmetry and the cube, we have always been interested in five-fold symmetry as well. It's just that it doesn't always work as well as four-fold symmetry.
Nature is replete with five-fold symmetry, thanks to five-petaled flowers. While most of the works of humankind are designed around 4-fold symmetry and the cube, we have always been interested in five-fold symmetry as well. It's just that it doesn't always work as well as four-fold symmetry.Our obsession with the number five clearly comes from our own hands, since we have five fingers on each hand. Our expression of the interest with the number five comes in several forms, though. My favorite is the five-pointed star.
Knowledge of the dodecahedron, a platonic solid bounded by regular pentagons, was actually kept secret in the school of Pythagoras. They believed that the general populace was simply not ready for it.
 The US military uses five-pointed stars to denote the highest ranks: admirals, generals, and commandants. The five-star symbol was created during World War II for Eisenhower and Nimitz.
The US military uses five-pointed stars to denote the highest ranks: admirals, generals, and commandants. The five-star symbol was created during World War II for Eisenhower and Nimitz.I read once where a draftsman invented the symbol for the US Government. But I haven't been able to find this information since. His designs were very interesting, to say the least.
The military loves the pentagon as well, as evidenced by their construction of one of the world's largest buildings: the Pentagon. It is remarkable that General Leslie Groves oversaw its construction. Earlier, he was put in charge of the Manhattan Project. So he was also in charge of the construction of another of the world's largest buildings, at Oak Ridge, Tennessee, used for the processing of Uranium.
Nature likes five-fold symmetry in part because five is a Fibonacci number and nature favors them. When I was a kid, I used to read the Fibonacci Quarterly religiously. I was like that.
It is notable that most music is rooted to four beats per measure. Sometimes, as in a waltz, we use three or six beats per measure. But five (or ten) beats per measure is exceptionally rare, except in Jazz. The Dave Brubeck Quartet made this famous in their rendition of Take Five. You can also hear this uncommon beat in the catchy original Mission Impossible theme, written by Lalo Schifrin (where ten beats is broken into two 3s and two 2s).
 For me, it is fun to see the way that pentagons, stars, and the rhomboids interact. You can make a rhombus with 72 and 108 degree angles. This is the one used to create the rhombic dodecahedron.
For me, it is fun to see the way that pentagons, stars, and the rhomboids interact. You can make a rhombus with 72 and 108 degree angles. This is the one used to create the rhombic dodecahedron.Put stars and pentagons together and they make an irregular tiling of the plane. The designs at Alhambra in Spain are great examples of the attempt to make a regular tiling from five-fold symmetry. But, if you only use pentagons, it really can't be done.
Here is a basic chart of how they fit together. The rhomboids trim out the design. Roger Penrose has constructed aperiodic tilings out of rhombuses, including the one I show here and also a sharper one with 36 degree angles in it. The golden section (1.6180334...) figures in all the shapes in one way or another. Quasicrystals can be made of these designs.
 Try to put pentagons together and you will have little luck in creating a seamless gapless tiling.
Try to put pentagons together and you will have little luck in creating a seamless gapless tiling.Here I have succeeded in putting some together using a star as a root and some crowns to glue them together!
The problem with the tilings stems from the angle of a pentagon: 108 degrees. The wide rhombus has an acute angle of 72 degrees, the complement of 108 degrees. The sharp point of the star is 36 degrees. So this means you get some other obtuse angles in there are well: 144 degrees for the thin rhombus.
A ten-sided regular polygon has outside angles of 144 degrees, the complement of 36 degrees. You can put a crown, three pentagons, and two thin rhombuses together and make a ten-sided polygon.
 This construction is often used in Penrose and Kepler tilings. Two such decagons can join and use a common thin rhombus.
This construction is often used in Penrose and Kepler tilings. Two such decagons can join and use a common thin rhombus.As I said before, the problem is that the primary angle, 108 degrees, does not evenly divide 360 degrees and so there must be some left over. After putting three pentagons together, exactly 36 degrees are left over.
So you must also have a star, a thin rhombus, or a crown to make pentagons tile the plane properly. If you distort the pentagon, however, you can solve the problem entirely.
 Here is the common way of doing this. It is a novel pattern, for sure! Notice the squat hexagons that intersect each other in perpendicular patterns.
Here is the common way of doing this. It is a novel pattern, for sure! Notice the squat hexagons that intersect each other in perpendicular patterns.This pattern has been used to create concrete tilings in real life! It's cool that tiling patterns have real-world uses. Of course they occur in crystals all the time and so patterns are automatically embedded in the real world all around us.
It is worthwhile to peruse the images of Alexander Braun, an explorer of pentagonal tiling.
Monday, May 28, 2012
Drawing On Your Creativity, Part 4
 Just a small post on my birthday: a little present to you. In a world of Instagram snaps and Hipstamatic effects, actual hand work is undervalued these days, so I have sought a style for my blog posts which uses handmade illustrations. This also conveniently relieves me of the problems associated with copyright infringement.
Just a small post on my birthday: a little present to you. In a world of Instagram snaps and Hipstamatic effects, actual hand work is undervalued these days, so I have sought a style for my blog posts which uses handmade illustrations. This also conveniently relieves me of the problems associated with copyright infringement.Why Not Hand Illustrate?
All the logo work I have seen recently, for instance was done in Illustrator, a brilliant Bezier-spline-based tool for cleverly crafting the smooth edges of figures. And it has grown to be so much more, with its incredible control over negative and positive spaces. But, to me, there is a pleasure in crafting something by hand, shaping it, cleaning it up, styling it with real brush strokes, and hand-coloring it. There is so much more life in hand-illustrated artwork. Imperfection is simply part of the style.
 Hand Work: Bridging the Domains
Hand Work: Bridging the DomainsFor me, hand work always starts with real paper and a real ink implement. This used to cause me some worry: worry about making mistakes, blotting out a section, making a line too thin or too fat. But I have learned to just start over until I get something which is approximately right. I use this same approach in songwriting.
The reason for the "just good enough" approach is that I can edit it later using digital means. For music, perhaps I can use ProTools, Ableton, or even GarageBand to shape the final result and re-record overdubs. For artwork, I have confidence that I can make it right using similar hand work in the digital environment. Suddenly it becomes possible to rework "permanent" ink lines and even to erase them. Work that was simply impossible in the pen-and-paper domain. Suddenly, in the digital domain, we are in the world of undo and pure unadulterated color.
I use Painter with a Wacom tablet for this work, but, of course, it can also be done in Photoshop or any paint program with good support for a tablet. I also envision doing an increasing amount of work on my iPad. In the mobile environment I use a Wacom Bamboo stylus to do my drawing. Drawing with a finger, while interesting and convenient, is a bit restrictive and inaccurate. Especially with my big fingers.
For hand-drawn traditional artwork good scanner is always important for bridging these domains, and with this comes some tonal compression and re-interpretation of the colors of the work, which is why I stick to black-and-white for my sketches. This means that simple equalization and gamma correction can convert your sketch to something that becomes useful in the digital domain.
Hand Work Entirely in the Digital Domain
OK I lied. Sometimes my hand work doesn't always start with pen and paper. This is because there is also extreme value in starting in the digital domain and staying there. In this environment you have several advantages that are not present in the pen-and-paper domain. For instance: cloning.
A specific example is shown here.
But instead of cloning, this is more to the tune of using the original as a reference.
I proceeded by opening an image captured using an iPhone. Then I cropped it to a good size and brought the smaller image into Painter.
Once there, I created five serigraphy layers using Effects:Surface Control:Serigraphy. This mimics a silk screen process, and creates layers that I can move into any priority that makes sense.
Then I collapsed all the serigraphy layers into a single layer and proceeded to rework every edge in the layer, selecting colors, redoing edges using a tiger stripe look characteristic of woodcut or linoleum cut.
I had to introduce several new shadings where there was none before.
And I am left with a self-portrait in woodcut style. I would like to say that it only took a few minutes. But in fact it took several hours. Actually, I'm still not completely satisfied. I figure about twenty hours of work should do it. But who has time for that?
Labels:
artwork,
creativity,
drawing,
hand work,
Painter,
portrait,
serigraphy,
traditional,
woodcut
Subscribe to:
Posts (Atom)

