Seven

After my post on five-fold symmetry, I can hardly keep myself from writing about seven. It seems unlikely, but the number seven does have some surprising properties, which I will illustrate. For instance, despite being called an octave, the diatonic musical scale really consists of seven notes: C, D, E, F, G, A, and B. With a remarkable sense of synesthesia, some people like to think each note has a color to it. I have folded my concept of the colors of notes into a paper aperture for your amusement.

Musicians like Alexander Scriabin developed systems to assign colors to key signatures based on the circle of fifths. The famous Hungarian composer and piano virtuoso, Franz Liszt, had a famous quarrel with Russian composer Nikolai Rimsky-Korsakov about the colors of the various key signatures; they saw them quite differently.

Seven is an odd prime number. Because it divides evenly into 1001 (and 1001*999 is one less than one million) its reciprocal has a six-digit repeat block, and thus seven the first number to have a repeat block that has length equal to the number minus one. It is a noble prime.

999999 = 3*3*3*7*11*13*37

Note that 7 and 13 have six-digit reciprocals, but 7 is often associated with good luck and 13 is often associated with bad luck.

An odd, prime number like 7 would seem to be impossibly irregular until you try to lay out seven pennies upon the table, as I did when I was five or so. I was surprised that it made the most elegant, regular arrangement possible.

And the seven pennies introduced young me to hexagonal packing. You can see that seven hexagons can make a hexagonal cluster. This is because it is a hexagonal number. The numbers 1, 7, 19, 37, ... , expressed as

1 + 6*T(n)

(where T(n) is the nth triangular number), are called hexagonal numbers because they give the exact number of smaller hexagons that can be put together to form a larger hexagon.

The clusters themselves can be fitted together. into an elegant offset packing, here shown using my Tile Patterns application. And a little help from Painter.

When I constructed this tiling, I had to work it out by hand first before I could enter it properly into Tile Patterns.

Here is my sketch of this tiling, giving some indication of the way I wanted to see it. Perhaps if we had hexagonally-packed eyes like the honeybee, and saw everything in these patterns, we would make our homes like they make their honeycombs.

It is only because my eyes are not hexagonally packed, I know, that I couldn't quite get the proportions right.

The green dashed parallelogram shows the repeat block of the offset tile pattern. It is because I like to think in squares and cubes that I can see it.

Seven is an interesting number for cubes as well, because it is one less than the cube of two.

Here I have illustrated that concept for you. It's always easier to see it visually than to just read it, I think.

Put one cube in the missing corner and you can make a 2x2x2 block. Two cubed is eight. So this shows seven cubes. Plus, I like a good graphic!

When it comes to seven, we do spend a bit of time dancing around six and eight.

The first diagram I showed was a folded paper aperture with seven sides. Its outline is a seven-sided regular polygon, called a heptagon.

Connect the corners of a heptagon and you can make various forms of seven-pointed stars.

Many countries use five-, six-, seven-, and eight-pointed stars as their symbols. Normally there are the wide star and the thin star. The Sheriff's Badge symbol uses a seven-pointed star that's somewhere in-between the two.

Other than these I don't really know other ways that the seven-pointed star gets used. This illustration I have created is a mandala form. I have applied a little color so you can see the various shapes better.

Seven dots on a grid can be situated in several different ways. But if you look at seven as two times four minus one, then you can see how a corner of one square may be shared with the corner of another square.

Each number is unique and interesting. In music, there is more to seven than just the diatonic scale. There is also music that features seven beats per measure, like Money by Pink Floyd, Solsbury Hill by Peter Gabriel, and the final Precipitato from Prokofiev's Piano Sonata No. 7 in B-flat. When I get in a mood, I will use this time signature. Usually it is broken up into two-two-three.

Finally, did you know that graph theory is based upon Leonhard Euler's solution to the problem of the Seven Bridges of Königsberg? Walk through the city, crossing each of the seven bridges exactly once. Once again the number seven provokes thought. Euler abstracted the two sides of the river and the two islands into four nodes and the bridges were thus abstracted into the seven arcs between them. The number of arcs attached to each node is called the degree of the node. If a node has even degree, then any path can enter and leave the node in an equal pairing. But if a node has an odd degree, then either the path must start or end there. It is easy to see that if more then two nodes have odd degree it is impossible for a single path to traverse all nodes, using the arcs between them. This is because a path must have only two endpoints. Königsberg's graph has four nodes of odd degree. Thus no such walk can exist.

So the number seven was actually the doorway to graph theory in the eighteenth century!

Patterns, Part 6

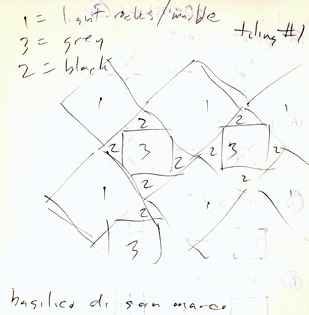
Tiling patterns are the subject of an application I have written specifically for exploring the San Marco Basilica tiling patterns I recorded in my notebooks in May, 1997.

The original tilings were simply sketched. This is not because I was without a camera. I certainly had a very good one with me. No, I sketched the tilings by hand because the church authorities would not allow photographs in the Basilica!

What mathematicians and others have done is to buy the post cards (I think I have a few of them as well), scan them, and post their pictures online. Usually as a challenge for students to determine which repeating group is represented in the tiling.

You can find all about the regular pattern repeating groups in the Handbook of Regular Patterns. My copy of this book is well dog-eared.

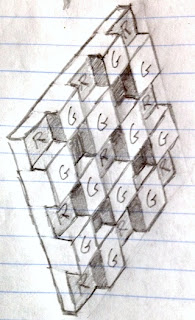
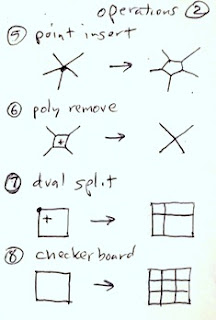
The pattern of five-square C-tiles from an earlier post of mine, Different Perspectives, is seen here. This was an early test case for my new application, which I call Tile Patterns.

This C-tile is one of the twelve pentominoes. All of the pentominoes can tile the plane in one way or another, though some of the tiling bases are a bit larger than this one.

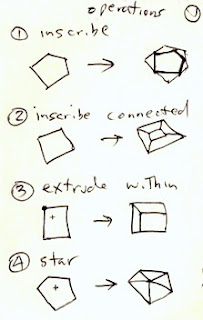
For information on the grid, basis, and segments used to define the tiles, consult my last post, Patterns, Part 5.

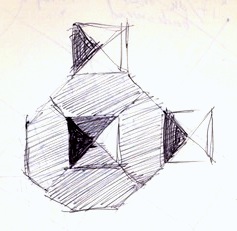
My test cases for this application make pretty designs. And some are rather busy in an op-art fashion.

Here is one, which has tiles that seem to simulate cut jewels, which must certainly qualify as a 1990's video game background!

This one broke my program a few times before I got it to work. Mostly because some of the polygons actually have holes in them!

Since the last post, I have implemented a few new things. Before, the application had the ability to set a grid, adjust and specify a basis parallelogram, and draw segments. As you draw, segments appear in all repeats of the basis area.

I have added the ability to divide up the segments when they touch or cross. Then I extracted a set of nodes (all on grid points) that bound each segment. Then I added the code to identify all closed polygon areas. As I mentioned, this includes some holes as well, particularly in the jewel tiling. Finally, the ability to specify the color for each closed polygonal area has been added. This allowed me to create all the tiling patterns you see here.

When I work this way, I only have to specify each polygon's color once, and all repeats of that polygon get colored. So I don't have to (laboriously) do the coloring in Painter. I get a cleaner result also. With this tiling, you can just see the parallelogram basis in red. Oops, I left it in!

Each of these patterns represents a new test case that broke the new application in some way.

The ability to save and restore patterns was the first feature I made. Then, when I built the extraction of polygons, I had to write save and restore of the polygons and their colors. This was an exercise in versioning, since I had saved several patterns already, but only the segments were stored.

Really what is needed (beyond what I have written so far) is the ability to maintain a palette of colors that is easy to pick from. And an easy way to deposit color into the polygons, with just a click.

The traditional way of doing this, along with adding segments, is a toolbox. Which is kind of passé, when you look at modern multitouch UI.

The ability to edit segments (in case I make a mistake) was another important feature to add.

Without that feature, I would have to clear and start over. Very troublesome!

So a segment selection and adjustment capability was necessary to implement. The requirement was either moving the entire segment or moving one of its ends. I just snapped the mouse point to the grid and looked for a segment end at that point.

For picking in the middle of a segment, I used a pick tolerance (really just a few pixels) to decide if I was close enough to the center of the line to pick it. Still, I had to implement point-to-segment distance, which is the only hard geometric computation.

Having implemented Shapes as part of Painter (and part of ColorStudio), I am very familiar with grid snapping and geometry editing. Actually very little coding was required.

I also used the San Marco Basilica tiling patterns as test cases. The first few patterns are really not as three-dimensional as some of the patterns. I think these were some of the first patterns laid down on the Basilica floor.

This pattern shows a black field with interspersed gray and light brown rectangles. Or you could view it as a checkerboard with turned gray squares inside the black ones.

The challenge for the tilers was to create diamonds that are just rotated squares. The larger light brown diamonds have an edge length that is sqrt(2) times larger than the smaller gray squares. That must have been fun.

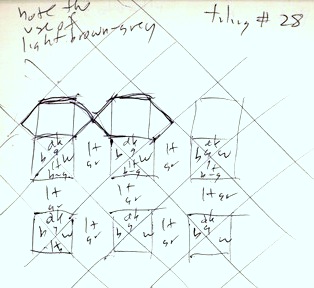
The next pattern shows a lattice design.

This design has a brown field with small black squares inside it. Each black square has a gray diamond inside it.

Clearly, the later the tile work was designed, the more complicated it becomes. Notice here that the brown field is actually made of hexagons that interlock. It's hard to show that here, though.

In the real Basilica, the tiles are all made of marble. So there is a strong texture to all of them, and also quite a bit of color variation.

That may be the next thing for me to implement, to simulate the marble texture. Of course I have some ideas on how to do that. Also, simulating the grout will be of importance. That turns out to be pretty easy, since I already have a way to render that (as I showed in the previous post).

With this one, the patterns are getting a bit more three-dimensional.

There's just the suggestion of a square box with a white bottom. This is inside a kind of square corner.

Of course, all the tile work is two-dimensional since it is just a floor.

The tilers took on the challenge of making their work more and more three-dimensional with time. By the time we get to the renaissance, most of the designs were faux three-dimensional designs, as we will see with later examples. Perhaps this one is more like a coat of arms.

The next one shows a feature that is quite common on the Basilica floor: the checkerboard.

Checkerboard occur most commonly in frieze work (borders) and often go around curves on the Basilica floor.

This shows the artisan's skill more than ever.

This pattern is found on the floor, along with some that only feature four checkers on a side.

I figure the high contrast of the checkerboard was a visual stimulant. But in reality, the tilers were influenced by what they could get from the quarries. In the year this was made, there was probably a surplus of white and black marble.

No patterns on the Basilica floor are more striking, or more difficult to create, than the ones that feature circles.

Here I have approximated the circular arcs with polygons, but you get the picture.

The really cool thing about this one is the way the circles intersect each other so perfectly.

Oh, and by the way, you see the pattern is incomplete at the top. Its another bug I'm chasing! You will see this on three or four of the tile images in this post.

Nonetheless, this image shows the magic of tile patterns.

This shows another kind of tile pattern. I think the design has the downwards diagonals in a kind of three-dimensional design to indicate some kind of depth.

And traditionally, the black field allows you to see the other elements as objects on that field.

In this case, the black is less used for shading than for simple depth.

This is another example of a half-drop pattern, as it would be called in Painter. Half-drop patterns are typically used for wallpaper. But wallpaper is really not very long-lasting. Not compared with a marble tile floor, which has been known to last thousands of years.

This pattern was featured in my last post. Here the colors are a little closer to the actual pattern taken from the Basilica floor.

With this one, the illusion of depth and three-dimensional structure is excellent.

The black diamond tile is used to show the inside of a box. The top of the box is shown in two colors, giving it a kind of silvery sheen. The side of the box is in natural wood colors. In all, it is an exquisite pattern.

This one was probably sixteenth century.


This next pattern shows clearly the three-dimensional structure.

The rendering of this pattern also shows clearly the grid at the top, the guide lines, and then the tile colors below.

Actually this is a bug, but I find it to be instructional.

With this pattern, the gray diamonds are the bottom of diamond-shaped pits. The white rectangles are the tops of the lattice. And something new: black diamonds form the intersections of the lattice.

It is visually interesting and also something quite new. Each tiling shows the style of its creator. It shows that the Basilica floor was designed by many artisans over the centuries, and that they were influenced by each other.

This tile pattern is an exquisitely detailed one. It is entirely three-dimensional. One thing about these tilings is that they have the concept of an assumed light source.

This imposes a rule that allows the designer to consistently shade the shapes. Of course this means that several different colors of tile are needed. In varying quantities also!

Various pyramidal shapes inhabit this one and so you see it is a different kind of surface depiction than we have seen so far.

Like the black diamonds of the previous tiling, this one features smaller pyramids (or indentations?) at each intersection. So most likely this one was created after the previous one.

Minecrafters will probably recognize this pattern: the corner cube pattern.

It was certainly not invented in Minecraft, which certainly appeared a few centuries earlier on tile floors in Italy.

It shows most clearly that consistent shading is required to get the best illusion of three-dimensional shape.

This is one of my favorite patterns due to its simplicity and its optically convincing form.

So this pattern is one of the more mature three-dimensional forms, rivaled closely by the next pattern.

This pattern is like the previous, but entirely in pyramids.

Ever seen the pyramids at Giza in a satellite reconnaissance photo? What I want to see here are the shadows of each pyramid being cast on their neighbors.

Well, perhaps that was beyond the thirteenth-century tile masters.

One thing needs mentioning. The tile patterns are quite similar to modern quilt patterns. I have even seen some of the San Marco tile patterns worked carefully into quilts (even with the marbled textures in the cloth). I can imagine them in latch-hook rugs as well.

I think this tile pattern shows that the tile masters were both aware and interested in shadows. The black triangle could be one facet of the three-dimensional geometry. But I think it's a shadow.

I see it as a shadow being cast into the trough that has been carved into the floor only in dark squares of the checkerboard pattern.

Walking on a floor with this kind of tiling, or in fact any three-dimensional depiction in a tile floor, would be a trip!

Literally. I would be worried about getting my foot caught in the apparent holes!

I found many depictions of this pattern on the floors in the old churches of Byzantium. This one differs from the earlier one both in color (four colors are used, subtly) and also in the angles of the squares.

Thus also in the width of the diamonds. They liked to use sixty-degree angles, so the diamonds would be "double triangles".

This one is shown at about fifty degrees. Mostly because I used a relatively small grid to construct it. It almost reminds me of the harlequin pattern, which is really only a diamond grid in a two-tone checkerboard. When you shade it in this way, it becomes three-dimensional, and can fool you into thinking it is a real surface.

This ornament is found on the floor at the San Marco Basilica. It is quite complex!

It reminds me of the American Indian rug patterns found at the Ahwahnee hotel in Yosemite.

But the Venetian tile floor will be still there long after the American Indian tapestries have turned to dust.

Unless, of course, global warming takes its toll and submerges the Piazza San Marco in the Adriatic.

In the meanwhile, let's keep the art and science of tiling patterns alive!

Patterns are a part of our lives. Our clothes, our wallpaper, our tapestries and hangings, our rugs, and many touchstones in our very existence show the influence of art and mathematics. The art of making patterns promotes spatial reasoning and creativity.

These are some of the reasons that I have featured textures and patterns in my blog. Also, of course, they dazzle our eyes and provide for wonderful illusions: the illusion of depth, the illusion of interlock, the illusion of spatial connectedness and completeness.

When a tiling pattern has a flaw, we automatically see it.

Patterns are literally built right into our consciousness.

Patterns, Part 5

I have decided to write an application to help me return to the original subject of this series of posts: tiling patterns. As you may remember, I was once impressed by the amazing floor of the San Marco Basilica in Venice. The floor is laid out in tiled marble, using a style referred to as Opus Sectile.

In one of my notebooks, I carefully transcribed the design and colors used by the tiles. You see tiling number 7 here, a wonderful pattern rendered in approximately the same shades as the original.

My first attempt at writing a tiling application became the origin of my San Marco series of applications that also saw the construction of the Painter 6 brushes.

For this app, I have simplified the method of how the patterns are constructed. First I lay down a square grid, similar to grid paper.

Most everything can be laid out on a grid. But grids may lead to inaccuracy of aspect ratio and relative sizes of the tiles. So I created the provision for doubling the grid in place on demand. This takes care of the need for additional accuracy and still keeps grid snapping.

Constraint-based systems make things easier, usually. Here is an example of the grid. All the examples are shown at 50% scale.

The next thing is to allow a basis to be designed on the grid.

A basis is a parallelogram that defines the repeat block of the tiling pattern. This repeat block can be any parallelogram shape.

Here it is a rotated square. You will see why the basis is required in a moment.

You will first notice that the basis is defined on the grid. It really consists of an origin and two vectors. One vector, (3, 1) defines the X axis of the basis, and the other vector (-1, 3) defines the Y axis.

Now, in my previous attempt to design a tiling program, I concentrated on a limited set of graph-theoretical operators. Upon reflection I have decided that this is too limiting.

Instead, I rely on simply drawing lines.

Here I draw a single line intersecting the origin of the basis (at the bottom) and extending over the entire width of it. This line gets replicated into all its instances: there is one for each repeat of the basis within the plane.

All the lines are constrained to fall on grid points. This turns out to be handy when it comes to making the line segments meet.

This tiling pattern only requires two lines, it turns out

The second line passes through the opposite (upper right) point of the basis and extends over its entire height.

It also gets replicated into all its instances. Each instance is defined to exist at one of the copies of the basis as it tiles the plane.

Together these lines form the tiling pattern. In this case, the pattern is a 3 by 3 square and a 1 by 1 square, perfectly fitting together.

Because the basis has edges that are length sqrt(10), and because it is square, the repeating elements in the tiling pattern must have area 10 square grid units by definition.

Next, I can remove the grid and basis, change the lines to black, and render it to create the desired tiling pattern.

I have chosen this tiling pattern to start with to show a useful kind of repeat that doesn't fall into the class of patterns easily designed in Painter.

In Painter 4, which was released in November 1995 (a very crucial period in my life!), I implemented the means to paint directly into a pattern and achieve seamless results. This included rectangular patterns and also patterns with horizontal and vertical half-drops.

In this new program, these kinds of patterns can be easily designed, but also both a horizontal and a vertical offset can be applied simultaneously. Sure, this kind of pattern could be designed in Painter. But you would need a square that is ten units on an edge to create it. Well, you could use a half-drop by using a rectangle that is ten units high and three units wide, and a half-drop offset of ten percent. But these are much messier ways of defining the pattern.

I bring the rendered tiling pattern into Painter so I can apply coloring to it. This gives me some ideas for new patterns.

But ideally I would do this inside the new program, which I call Tile Patterns.

It is easy to design a number of patterns using this fresh approach.

You might assume, just because the basis is a parallelogram, that it wouldn't be possible to design triangular shapes, hexagons, or perhaps strangely interlocking shapes.

That would not be a correct assumption. Here a triangular pattern is designed using the grid and a parallelogram whose shape matches the appropriate shape (two triangles attached).

So in this case, the repeat pattern is actually two triangles.

Here I have used an approximation for sqrt(3)/2 which I arrived at using continued fractions. The actual number is 0.8660254... but it can be successively approximated by these fractions:

1/1, 6/7, 13/15, 84/97, ...

I have chosen 6/7, an approximation equal to 0.857... to represent the irrational number, so it's only off by about 1%.

Hexagons can also be designed using this program. Here I am using the same rational approximation to sqrt(3)/2. As with the triangular design, this design uses three lines (which you can see inside the basis parallelogram).

But, unlike the triangular design, the area of the basis is equal to the area of the hexagon.

So far I have only shown convex shapes, but it is also possible to design interlocking concave shapes. This is another kind of interlock, of course, but one which is cyclical in another way: in a lattice.

Consider this pattern. Here I show interlocking plus symbols.

Yes, as you can see, the area of the plus symbol is five square grid units, and so the basis rectangle also has the same area, with edges that are sqrt(5) in length.

I can design interlocking patterns just as easily, but it does take a bit of planning beforehand.

I like to sketch out the pattern first and then draw the basis on top. This gives me a blueprint for how to proceed inside the Tile Patterns program.

Here you see a simple interlocking pattern.

You can see it is designed on the same basis as the first pattern I showed. There are an extremely large number of patterns on this one basis alone.

Tiling is an intellectual exercise. When I was younger, I used to buy grid paper in hexagons and triangles and then color inside the tiles to make patterns. You can see one of these in my three-dimensional thinking blog post. So in the same vein, I color the tiling patterns I create, looking for novel color combinations.

Here is an example of this kind of fun.

Sometimes I just line to make patterns that show color and delight the eyes, and sometimes I am in it for the pattern: really more of a contrasty dotted kind of thing.

It is useful to realize that the tiles do not have to fill the entire space within the plane. I can create individual structures with some separation in between them to give a kind of hand-designed formulation.

In Painter, I can soften and increase contrast (anneal) the pattern to get rounder forms when I want.

This is the technique I used to create this new pattern, a candy-coated array of dots.

They are quite pleasant!

I am not sure where I want to go with this application in the future. Most likely the next step is to have the app automatically enumerate the closed shapes that define the repeats (though, as you can see, there might not be any closed shapes, as in the case of the maze pattern below).

It seems like a merging of the San Marco application capabilities with the line-drawing capabilities of the new app would be a good way to proceed.

Perhaps a nice way to save out tiling patterns as Painter patterns would be useful.

As I referred to earlier, the ability to color the tiles inside the application is a capability I will code up very soon.

Here is a pseudo-maze pattern I have created using this application. This shows that I can control the thickness of the lines when rendering them in black-on-white.

And the final pattern I will show is another tiling pattern from my notebooks on the San Marco Basilica.

Of course the grout spacing is nearly zero in the actual Basilica floor. Those artisans in the twelfth century were actually quite good!

Painter's Image Hose

In Painter 3, a new kind of brush was added: the Image Hose. With this tool, you could draw using random snippets of image data. Each bit of image data could be individually masked and even shadowed. So you could literally paint with reality. To right, I have included an image created with Corel Painter 12. First a background of dirt was drawn with the image hose, and then some leaves we're drawn on top, also with the image hose.


How did the image hose begin? John Derry and I were sitting outside at a Restaurant in Chicago on July 31, 1992 and he suddenly wanted to be able to paint with the tree. I considered this for a while, and then i took down a note. My note said: analyze and grow texture from an example. But how??


Imagine each of the tree's leaves had a picture and they could be placed randomly. I remember we came to the conclusion that with only a few leaf pictures and perhaps some randomness of rotation angle or shading that you could paint a reasonable tree image. This was ideal since memory was, and continues to be, at a premium. In those days, that would be true on a Mac. In these days, that would be true on an iOS device, like an iPad.

The idea was in our heads that we could store a few images and draw using the set of images. So I came up with a way of doing it, which was initially called the structured clone.

As shown on the left, by October 1992 I already had some idea that the images could be stored in an array. Each element was individually w by h pixels, and they were arranged into a potentially three-dimensional structure. Each element is clearly spelled out to have an arbitrary 24-bit color image with an 8-bit alpha mask, treated like a penmask in the usual way.

A penmask is what we called the mask of a dab of paint. In those days, a brush stroke was always made up of a sequence of paint dabs placed along the bush storke's path. In this case, the brush stroke could be made up of a sequence of masked images instead.

I say it can be indexed by 0, 1, 2, or even 3 parameters - this is the dimensionality of the image hose, what I called the rank.
These parameters were such things as random, pressure, tilt, bearing, velocity, etc. In the random case, a new image element was chosen for that rank each time a new dab was placed along the stroke.

Let's imagine an example. I create 36 images in a 6x6 array. The rows contain six different orientations of a leaf, one orientation for each row. The columns contain six different sizes for each leaf, from small to large. I could use pressure to index the column, so the harder I press, the larger the leaf. I could use stroke direction or even stylus bearing to access the rows, which might allow me to control the orientation of the leaves by using my hand also. In this way, you could have more control over creating a tree just be drawing leaves.

Another thing we started doing was giving each image hose element a drop shadow. This meant that as you drew a pile of leaves, the leaves begin to shadow each other and thus shading would develop, making the pile appear to be three-dimensional.

To the right I have included a pile of randomly-oriented cubes created with the Image Hose in Painter 12. The drop shadow on each one is down and slightly to the right. This produces a slight shading below.

When we finished working on the Image Hose, we filed a patent in December 1995. You can find the details in the US Patent Office; it is patent number 5,767,860. It is one of the only things we decided to patent at Fractal Design, and so it is the only patent I share with John Derry.

Thoughts on How I Might Do It Differently


Today, there are quite a few different constraints on how things work, but compute power is much greater than it was in the early 1990s. The main thing I would do differently is to compute most of the changes on th fly. In Painter 4, we decided to do just that, computing scale, rotation, and opacity on the fly. But nowadays, I would probably allow for hue, saturation, and lightness changes, shadow depth, shadow opacity, and shadow feather to change on the fly as well.

This would mean that the only thing stored in the image hose database definition would be the random elements themselves. This would prevent much of the hand work in creating an image hose "nozzle".
It would be good to allow for 3D rotation and scaling as well. So that might mean creating a 3D definition for each element, which could be a bit complicated. The shading could also change on the fly.

I would probably allow for the nozzle to be made of several kinds of items, and separate them into groups. For example, you could make one group the stems, another group the leaves, and a final group the flowers. They would be stored into a single image hose nozzle definition. Then you might use pressure to choose between them, or you can hold down some modifier key, such as the command key or the command and open key to get each level when drawing.

Another thing I would like is to draw into a lens layer using an image hose, so that distortions can be applied s you draw. For example, you could draw shiny stones, then you could draw the water distortions on top to make the stones look like they are in a stream bed. And then perhaps the shines could be drawn on top as the sun sparkles on the water using another kind of image hose.

Something I tried but isn't still available in Painter is a grid-based image hose. This one draws each element inside a grid. You can randomly choose elements that are designed to connect with each other.

Here is an example of a tile design that could go into an image hose element and then placed randomly. Each element is designed to match at top, left, bottom and right, and so it won't matter how you place them, they will always match.

I would like to try this in square and hexagonal arrangements. Even in half-drop arrangements. It would be easy to design elements, since Painter supports drawing into half-drop patterns.

In this way, the image hose could help you to create mazes and other kinds of patterns that repeat, but without really repeating.

Patterns, Part 1

Patterns are found everywhere in nature, from the crystalline structure of the sodium and chlorine atoms in salt to the six-fold symmetry of snowflakes to the spiral arrangement of sunflower seeds. We humans make a habit of copying nature's patterns, and adding a few of our own.

As we saw in my post on image sensors, a very regular pattern of red, green, and blue photosites is employed to make up the Bayer pattern that nearly all image sensors use. The pattern of green pixels, for instance, resembles a checkerboard.

We take advantage of this pattern to create images using a process called demosaicing. This is the process of turning the mosaic of red, green, and blue pixels into full-quality RGB image data.

Behind the demosaicing process is an art so well-studied that it goes back into antiquity: mosaics. The Romans had two kinds of mosaic work. The first was called opus sectile and the second was called opus vermiculum.

Opus sectile is the laying of shaped tiles to create a beautiful regular pattern.

Opus vermiculum is the laying of tiny tiles (usually in rows) to create a picture. Each tile has its own color and the result gives us some of our oldest color portraiture.

San Marco Basilica

I once had a chance to visit the Basilico di San Marco in Venice, Italy. Inside it I found every kind of regular tile work I could think of, and a few more. So I took out my notebook and began sketching and detailing all of them.

I'll show a few patterns from my notebook. Tiling 1 has diamonds with inscribed squares. The colors give it depth.

I gave each color a number and gave each tile a number so you can color by numbers to get the actual tile pattern I saw at the Basilico. It was actually breathtaking, because there was hundreds of years of artwork located in one place. I could imagine the artisans passing the knowledge of their craft down from generation to generation. Each one had to add something new and novel.

In the case of tiling 28, there was something more than meets the eye in my flat sketch. The colors gave an appearance of three-dimensional form to the flat tile floor.

Here there is a base surround consisting of six-sided tiles all done in a light gray, and a center square, cut into triangles that appears to be a pyramid.

But this look only occurs because of the shading imparted to the square.

And that shading comes from the colors of the marble tiles that make up the floor itself.

I found it to be brilliantly designed.

Here you can see a hand-drawn image of it, but note that the bottom triangle of the square actually gets a little bit of brown-gray. This makes the pyramid seem a bit shiny, as if the black and white were shadow and specular shine, and the brown was the actual color of the pyramid.

It was little touches like this that drew my eye to each new tiling pattern.

I found and drew up 36 tiling patterns I found there. Yes, I am detail-oriented. But I have to say that the art of Byzantium really did capture my interest.

Another three-dimensional kind of shading was found in tiling 23. Here a lattice work is suggested, by an oblique grid set in white to bring it to the foreground.

Within each diamond in the lattice is a tessellation that makes it look like the diamond is really a rectangular hole. The base of the hole is black, and the two sides are set in various grays.

This is typical of the ingenuity of the Venetian craftsmen from the Renaissance and also from the Byzantine era.

The tiling schemes often employed this kind of optical illusion of shading and depth.

It so closely matches some of my sketch work, since I sometimes work in basic shapes.

This one is from Tiling 19 and once again has hexagonal tiles that form a lighter base.

But this time, the center squares are set as a black square with an inscribed white diamond.

I remember that the tour went on as I stood and took down every kind of tile pattern I could find. I had the sense that it would be quite creative to make a program that could create these kinds of tiles.

And, as the author of Painter, such things were my bread-and-butter. Plus, I wouldn't have created Painter if I weren't obsessed with art, craft, and patterns.

So, my approach was to find a way of factoring the tiling patterns into a kind of topological language, a set of operations that could, when applied in clever ways, produce all the San Marco patterns.

So, reproduced here is the set of topological operations I thought up that might be able to create the tile patterns.

For instance, let's try to make tiling 28 using operations. First start with a big square. Then apply operation 8, checkerboard, to make a bunch of squares inside it. Then, on each internal point where four squares meet, use operation 5, point insert, to replace the point with a diamond. Finally, on each diamond, use operation 4, star, to split the diamond into four triangles.

Then you can color each six-sided shape light gray, and go about coloring the four triangles inside the diamond so that they look like a pyramid.

Well, actually, I have created tiling 28 rotated 45 degrees, but you see the prices nonetheless.

The more places I went in Venice, the more operations I found might be necessary to create the tiling patterns.

To the left are two more operations I thought would be necessary to incorporate circular portions into the tiles.

Ravenna

After Venice, we went to Ravenna. This is a vertical Mecca for mosaic artists. The mausoleum of Galla Placidia is a total shrine to mosaics. After I had implemented the mosaic tool set in Painter 4, this was a necessary pilgrimage for me. 

In the modern day, opus vermiculum is used quite often when creating mosaics, just as it was in the middle ages.

Here we see part of a floor mosaic I found in Hawaii on the big island in Hilo.

It's use of color and the run-of-tiles technique is straight out of the Ravenna textbook.

Also in Ravenna, I found more opus sec tile work, tiled floors. The Byzantine artisans practically invented this kind of tile. So I got out my notebook again, and started cataloging all the tile patterns I could find.

The Byzantines did like the mirrored symmetries, particularly combined with tilted forms.

This particular pattern combines rotated squares in a pattern that is mirrored in both x and y, with thin diamond-shaped separators.

Painter Paper Textures

In Painter, all of the paper textures are designed as repeating tiles. The whole idea of repeating tiles is to create a tile where you cannot see a flaw at the edges. I spent inordinate amounts of time working out how to create those tiled paper textures without losing the punch of the texture. At the time, the standard way of making a repeating tile was to use one crossfade between the top and bottom edges and another crossfade between the left and right edges. But this technique always creates a loss of contrast of the paper texture. So I had to invent new techniques that just grew the tiles from scratch.

Some techniques used FFTs (Fast Fourier Transforms). This was convenient because 2D Fourier transforms automatically wrap around. Here's the formula: first salt an image with some kind of texture with a given desired spatial frequency, convert to the Fourier (frequency) domain, randomize the phase, and convert back to the spatial domain. Voilá! Wrap-around repeating tile textures.

Other techniques built wrap-around structures that were used to automatically create wrap-around tiles. Like a Voronoi pattern designed to exist in a wrap-around tile. Then fill the Voronoi tiles with texture. This was used to create the random hatching patterns. But it's complicated, so don't try it at home! You might waste a few years making it work.

Painter Mosaics

I Implemented mosaics in Painter 4, and to do it I had to solve the problem of offsetting closed polygons, and clipping of polygons against other polygons. This was required to create the grout.

For the occasion of the Painter 4 poster, I created a mosaic called the Miracle of the Paint Can. This took me about 36 hours of laborious work. And I was using beta software, so it crashed a few times along the way, which was quite a bad thing for me since I was on a deadline!

From left to right, I put the portraits of John Derry, Glenn Reid, myself, Tom Hedges, and Steve Guttman into the image.

Painter Mazes

The maze effect in Painter is designed to create a maze with no discernible pattern.

To do this, I create the maze in a binary representation and then expand it into a Painter bitmap. But to make the maze in the first place, I had to solve the problem of creating a proper spanning tree, randomly connecting spanning trees until there are only two trees. This is to ensure a single unique solution to the maze, from the upper left corner to the lower right corner. Try it!

I first implemented the maze algorithm in 1978 at Calma. It was after taking a graph theory course from Dick Karp at Berkeley, who has since won the Turing Award.

I Love Patterns

Like this raindrops pattern. One day it was raining and I took pictures of the sunroof of my car. I love how the raindrops avoid each other. It's so organic.

One more picture. This is a note from the Palazzo Pitti in Florence, Italy. It had a tiling pattern that comes from weaving. With the tiles apparently crossing over and under each other. But in this case, the "holes" in between the strands are colored white.

I'm not sure what they were getting at, but I like it anyway.